解三角形 解直角三角形(斜三角形特殊情况): 勾股定理,只适用于直角三角形(外国叫"毕达哥拉斯定理") a^2b^2=c^2, 其中a和b分别为直角三角形两直角边,c为斜边。勾股弦数是指一组能使勾股定理关系成立的三个正整数。比如:3,4,5。他们分别是3,4和5的倍数。从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少? つまり,三角形 a b c abc a bc は直角三角形。 この性質は タレスの定理 とも呼ばれます。 「円の直径→直角三角形が潜んでいるかも」と意識しておきましょう。
小学奥数勾股定理与弦图 直角三角形面积 勾股定理与弦图 奥数网
直角三角形定理
直角三角形定理-右図1のような直角三角形については、 a 2 =b 2 c 2 (1) が成り立ちます。(三平方の定理) では、図2のように∠ A が 90 ° でないときには、この定理はどんな形になるのでしょうか。直角三角形的性质: (1)直角三角形两个锐角互余; (2)直角三角形斜边上的中线等于斜边的一半; (3)在直角三角形中,30度角所对的直角边是斜边的一半; (4)在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°; (5)在直角三角形中,两条直角边a、b的平方和等于斜边c的平方,即a^2+b^2=c^2 (勾股定理); (6)在直角三角形中



勾股定理 快懂百科
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。直角二等辺三角形の底辺と高さの長さは同じです。底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。よって、直角二等辺三角形の辺の比は「1:1;√2」です。 ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c² 直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值。 三角形余弦定理的公式 对于边长为a、b、c而相应角为A、B、C的三角形,有: a2=b2c2bc·cosA b2=a2c2ac·cosB c2=a2b2ab·cosC 也可表示为: cosC=(a2b2c2)/ab cosB=(a2c2b2)/ac cosA=(c2b2a2)/bc
2 二等辺三角形の定義と性質・定理 21 二等辺三角形の底角が等しい証明; 1余弦定理公式余弦定义主要作用是依靠已知三角形的两条边及其夹角,求第三边的情况,如下图:这里我们不处理向量(矢量)运算,单纯的从标量数值长度的推算入手,建立垂线后,得到的 直角三角形 ADC,可以通过勾股定理 static void Main (string args 全等三角形定理 天奇生活 4、有两角及其一角的对边对应相等的两个三角形全等;5、斜边及一直角边对应相等的两个直角三角形全等。
どうも、Drリードだぞい。 中3数学では、 三平方の定理(ピタゴラスの定理) を勉強してきたよな? 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²+ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。 今回はそのための基礎トレーニングだ。直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度直角三角形是数学里最有用的形状之一! (例如,它用在 勾股定理 和 正弦、余弦和正切上。) 你来试试 (拉拽点a、b或c): 两种直角三角形 有两种直角三角形: 不等边直角三角形 一个直角 另外两个 不同的 角 没有等边 等腰直角三角形 一个直角



怎样算三角形的斜边长怎么算出三角形斜边长度 朵拉利品网



直角三角形斜边怎么算 360新知
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem)は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}} が成り立つという等式の形で述べられる。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。 ピタゴラス勾股定理 (英語: Pythagorean theorem / Pythagoras' theorem)是 平面几何 中一个基本而重要的 定理 。 勾股定理说明, 平面 上的 直角三角形 的两条直角边的长度(古称勾长、股长)的 平方 和等于斜边长(古称弦长)的平方。 反之,若平面上三角形中两边长的平方 关注 展开全部 直角三角形的判定方法: 判定1:有一个角为90°的三角形是直角三角形。 判定2:若a²b²=c²的平方,则以a、b、c为边的三角形是以c为斜边的直角三角形(勾股定理的逆定理)。 判定3:若一个三角形30°内角所对的边是某一边的一半,那么这个




直角三角形の辺の長さ 合同条件 面積について アタリマエ
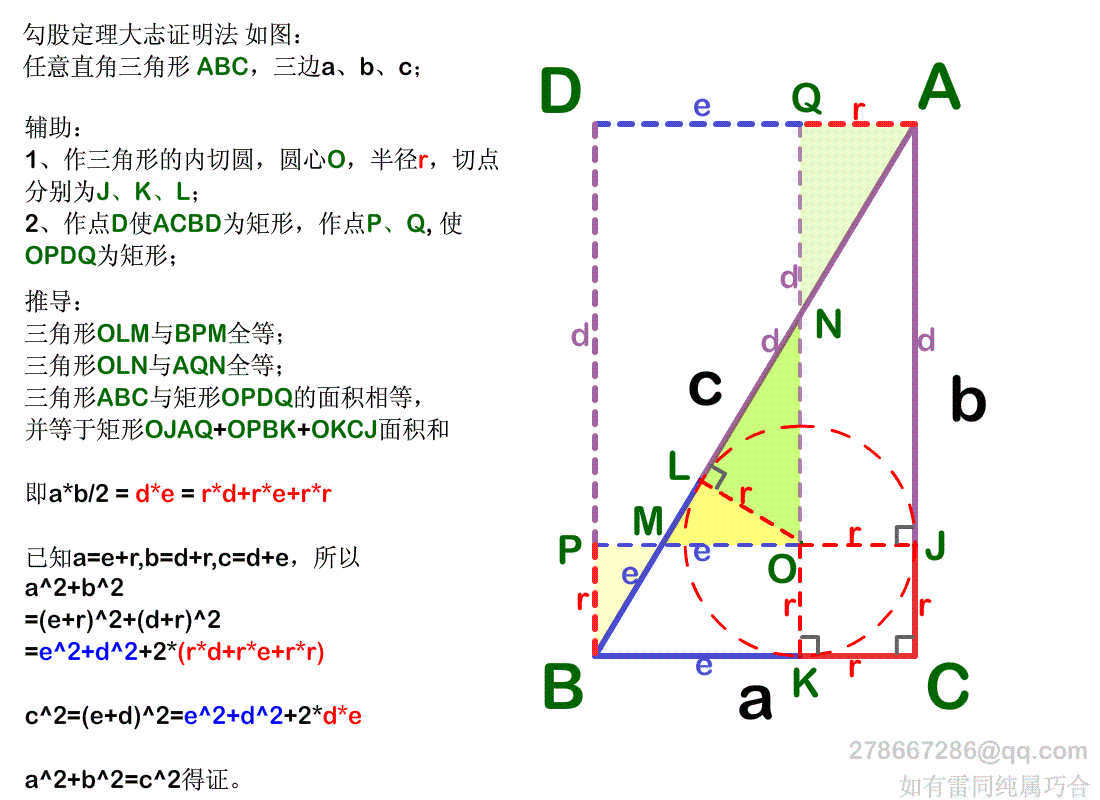



一不小心 发现个勾股定理证明方法 大志的博客 Csdn博客
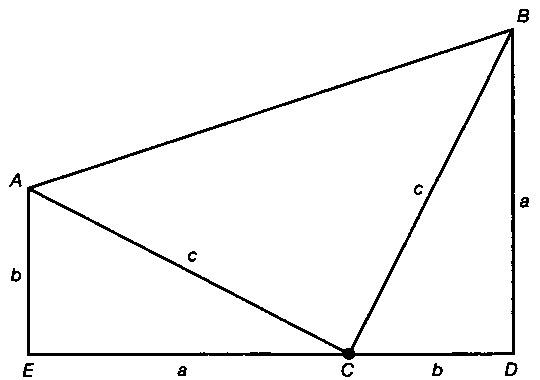
直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。 三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。直角三角形bcdに三平方の定理を用いると, CB 2 = CD 2 BD 2 ・・・・・・(1) CB = a , CD = b sin A (⇒ ここ を参照), BD = c − b cos A の関係を(1)に代入すると



新孔夫子 畢氏定理教學網站上網摟




直角三角形知道两边求角度 每日一讲 解直角三角形 3 21 半次元的博客 程序员宅基地 程序员宅基地
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し 三平方の定理 直角三角形の直角を挟む \(2\) 辺の長さを \(a, b\) とし、斜辺を \(c\) とすると \begin{align}a^2 b^2 = c^2\end{align} 三平方の定理とは?証明や計算問題、角度と辺の比の一覧三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。
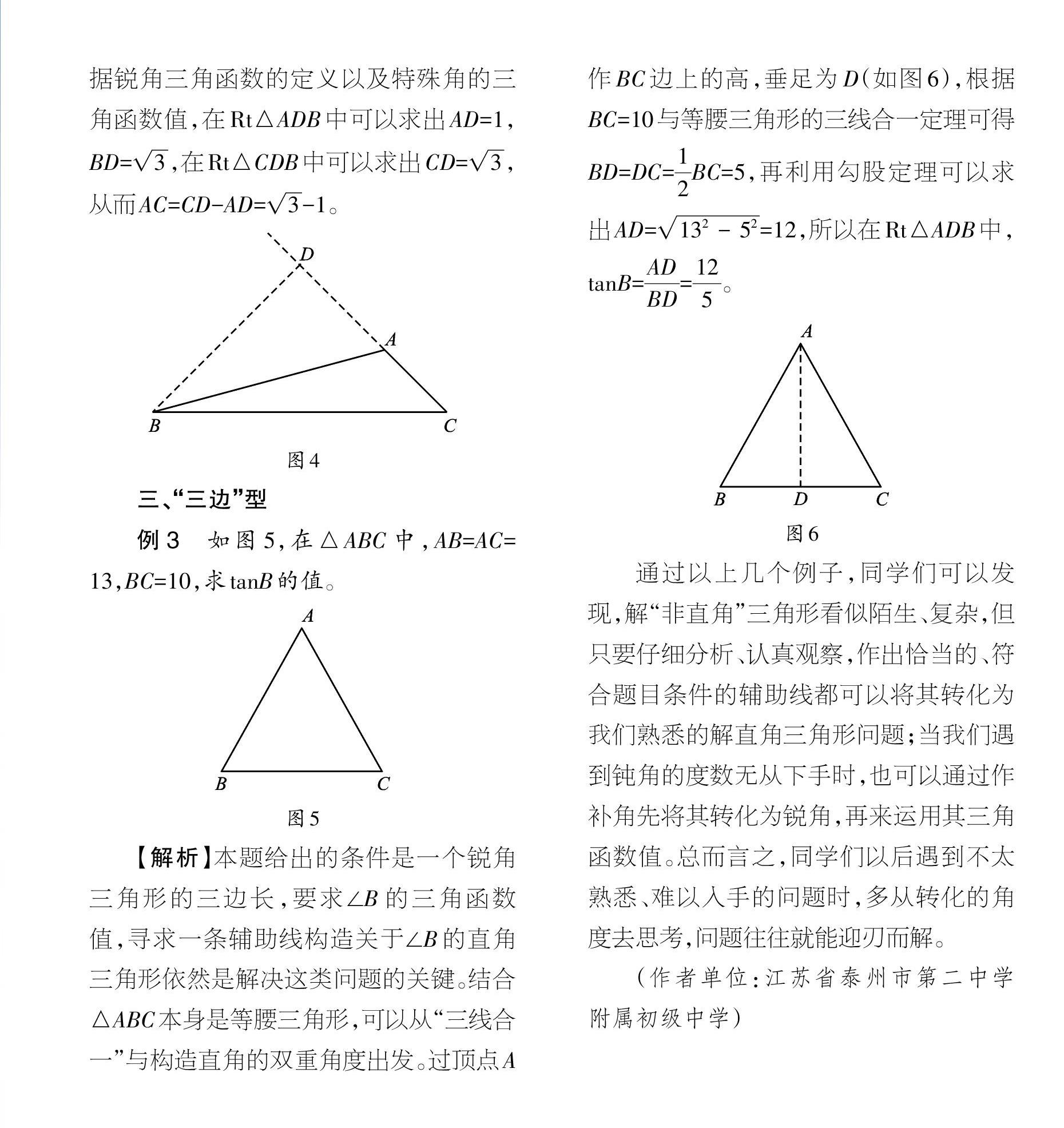



你会解 非直角 三角形吗 参考网




直角三角形 Wikiwand
球面直角三角形のピタゴラスの定理( 2 C の直角三角形ABC について) (A)cos cos cos (B)sin sin sin A ,sin sin sin B (C)cos cos sinA B ,cos cos sinBA (一般の)球面三角形ABC における正弦定理・余弦定理 正弦定理 sin sin sin sin sin sinA BC3、直角三角形中, 斜边 上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点, 外接圆 半径R=C/2)。 该性质称为 直角三角形斜边中线定理 。 4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。 5、如图2,Rt ABC中,∠BAC=90°,AD是斜边BC上的高,则有 射影定理 如下: 图2射影定理图 (1)(AD)²=BD·DC。 (2)(AB)²=BD·BC。 (3)(AC)²=CD·BC。 射影3 直角三角形の性質と斜辺 31 直角三角形の合同条件;




自己对勾股定理的一个证明 骰间宇宙的共享空间



第一章 1 2 直角三角形课时二 2 直角三角形 北师大版八年级下册数学课件 数九网
余弦定理を用いた判定法 三角形の $3$ 辺の長さが与えられた時,その三角形が鋭角・直角・鈍角三角形のどれであるかを判定する方法を紹介します.直角三角形の合同条件 直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明) まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。



中考数学专题复习 第18讲直角三角形 吉祥日历



初中数学 18勾股定理 001两个特殊的直角三角形求边之比 哔哩哔哩 つロ干杯 Bilibili
直角三角形性质 直角三角形是一个几何图形,是有一个角为直角的三角形,有一般 的直角三角形和等腰直角三角形两种。特别性质有: 1、勾股定理,直角三角形两直角边的平方和等于斜边的平方。 2、在直角三角形中,两个锐角互余。重要 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、このタレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。ターレスの定理、タレースの定理ともいう。 歴史




直角三角形知道两边求角度 每日一讲 解直角三角形 3 21 半次元的博客 程序员宅基地 程序员宅基地




初二数学 直角三角形 学习目标和经典例题 数学老师手写教案 网易订阅
三角形,又稱三邊形,是由三条线段顺次首尾相连,或不共線的三點兩兩連接,所组成的一个闭合的平面图形,是最基本和最少邊的多边形。 一般用大写英语字母 、 和 为三角形的顶点标号;用小写英语字母 、 和 表示边;用 、 和 給角標號,又或者以 這樣的顶点标号来表示。直角三角形fhgを用いてfgの長さを出す。 そのためにまずhgの長さを求める。 dgc≡ dfeなので、gc=fe=fa、fd=gbである。 ef=xとすると、fd=8x, ed=4 直角三角形efdで三平方の定理を使うと x 2 4 2 =(8x) 2 x 2 16=6416xx 2 16x = 48 x=3 af=3、fd=5よりbh=3, bg=5なのでAma02 練習問題へ u adc は直角三角形であるから,ac の長さがわかればad の長さが求められる。 そこで,ま ず,u abc に注目し,三平方の定理を利用して,ac の長さを求める。 u abc で三平方の定理より ac 5 5 10 5 cm=-=()_i2 2 ←ac ab bc=-22 さらに,u adc で三平方の定理より




Xm9lgcox98ortm



由边的数量关系识别直角三角形 定理的应用 16 2由边的数量关系识别直角三角形 初中冀教版 数学中国网




直角三角形的性质与判定定理



八年级上册第二章第六节第二课时 直角三角形 数学跟我就行 微信公众号文章阅读 Wemp



勾股定理 科普中国



12岁的爱因斯坦 是怎么证明勾股定理的 杭州新闻



直角三角形 信息图文欣赏 信息村 K0w0m Com




勾股定理的证明方法5种




北师大版八上数学1 2 一定是直角三角形吗 课件 共21张 下载 Ppt模板 爱问共享资料



1
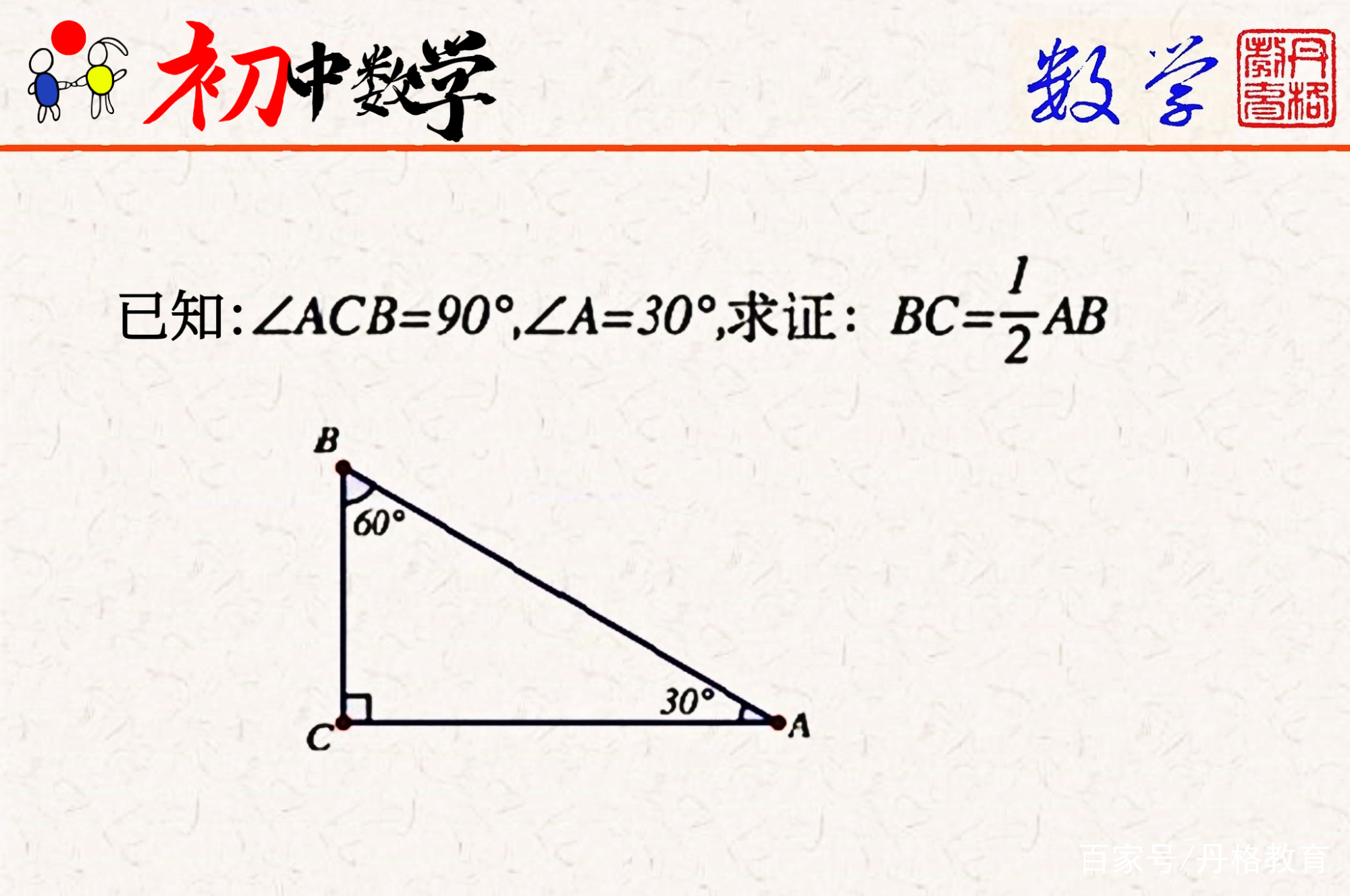



初中数学证明 求证直角三角形中30 所对直角边等于斜边的一半 来自百家号 丹格教育 不错网




數學一點也不無聊 教學活動 直角三角形拍賣會 搭配單元 二上畢氏定理 失敗版本



初中数学 直角三角形斜边中线定理的证明 一种相对简单的方法 已知 Abc是一个直角三角形 Ab D是ac中点 求证 1 2ac 海燕数学 哔哩哔哩
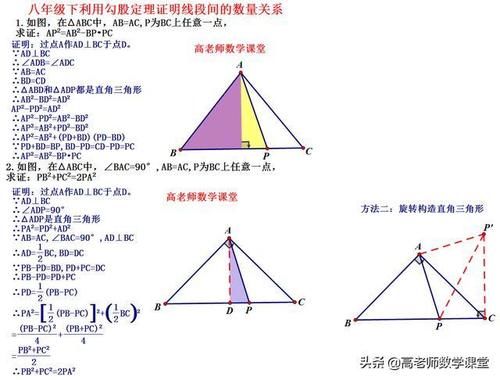



如何证明直角三角形




从广勾股定理到斯蒂瓦特定理再到三角形重要线段计算公式 每日头条



一定是直角三角形吗 勾股定理ppt下载 第一ppt




直角三角形 维基百科 自由的百科全书



三角形求斜边直角三角形求斜边长计算公式 朵拉利品网



直角三角形的高怎么画 信息图文欣赏 信息村 K0w0m Com




八年级数学直角三角形课件苏科版课件下载 Ppt模板 爱问共享资料
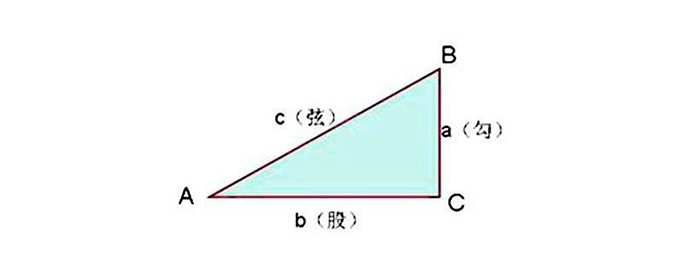



勾股定理怎么算 科普 常识知识




直角三角形边角关系 华夏文明



初中数学 勾股定理 50道经典例题2 北京市第四中学自由行热门攻略 中考 辣妈 初中数学 教育 中学教育
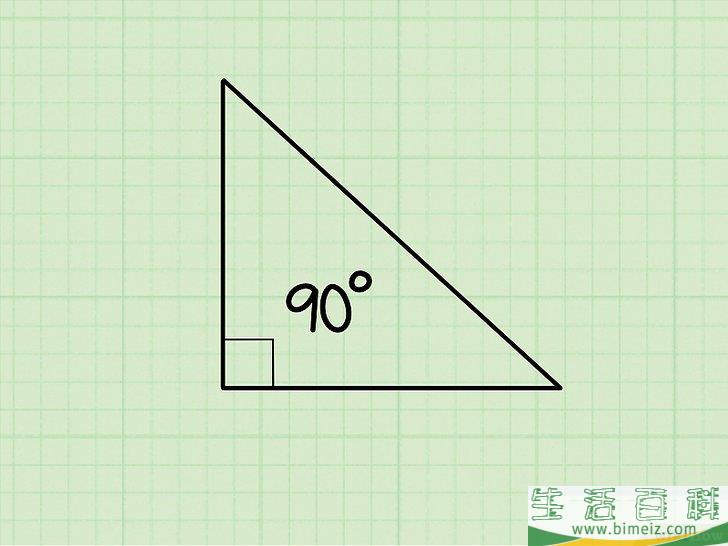



如何使用勾股定理 生活百科



小学奥数勾股定理与弦图 直角三角形面积 勾股定理与弦图 奥数网



一定是直角三角形吗 勾股定理ppt下载 第一ppt




微博搜索
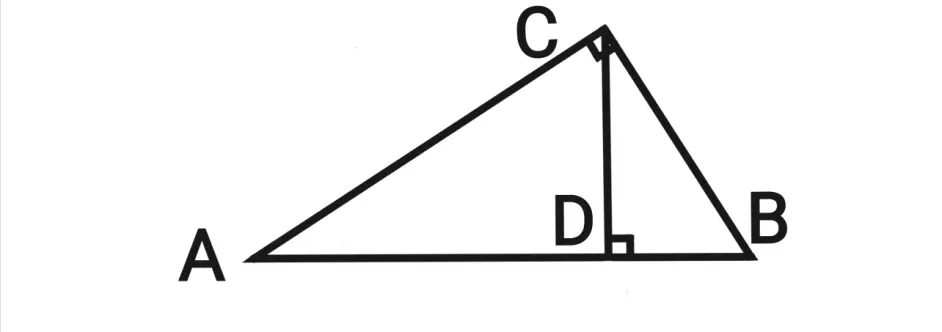



Koaz57uwiskrgm



勾股定理 快懂百科




角平分定理直角三角形 三角形png图片素材免费下载 图片编号 Png素材网




直角三角形面积 周长 夹角 勾股定理 毕达哥拉斯在线计算器 三贝计算网 23bei Com



直角三角形斜边中线定理 初三网




直角三角形的斜邊 翰林雲端學院



直角三角形求斜边边长 西瓜视频搜索
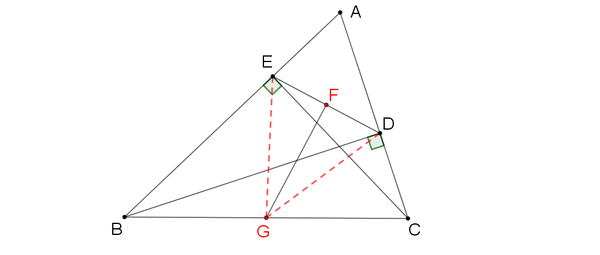



初中数学几何模型之中点模型例题 2 直角三角形斜中线定理的妙用 知乎




勾股定理應用2特殊直角三角形的勾股定理比例 Youtube




初中数学 勾股定理小课堂 精准命题 精准命题 大智教育 中小学课外辅导




直角三角形邊長求角度直角三角形 Itha



直角三角形三边长度 图片欣赏中心 急不急图文 Jpjww Com



数学百科 直角三角形斜边中线定理 数学尖子生题库 微信公众号文章阅读 Wemp
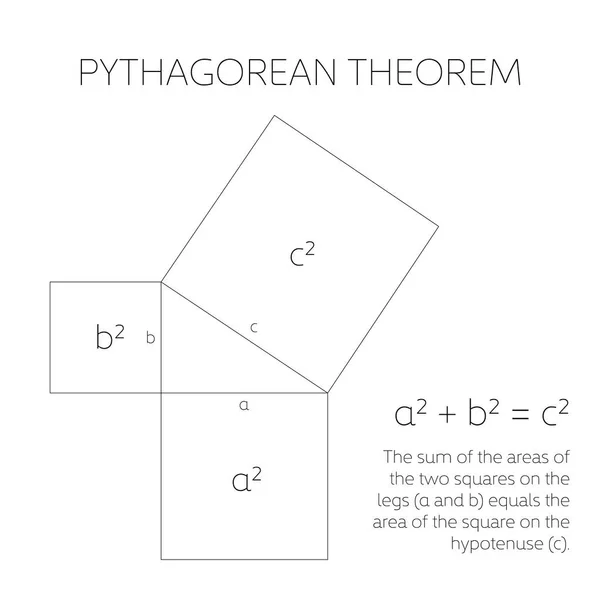



直角三角形的斜边图库矢量图片 免版税直角三角形的斜边插图 Depositphotos




射影定理 维基百科 自由的百科全书



四直角三角形的射影定理 人教版高中选修4 1数学电子课本 数九网



现在考考你勾股定理 你还会



直角三角形怎么求斜边直角三角形求斜边长计算公式 朵拉利品网



30度60度90度勾股定理 30度 60度 90度的直角三角形三边的比例关系 朔旭金融网



几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角的三边关系定理 西瓜视频搜索



1
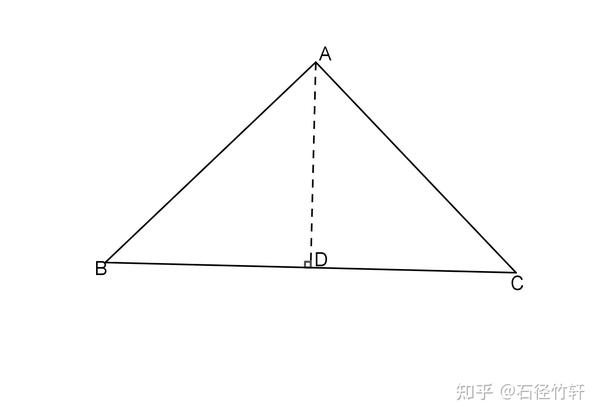



非正经数学 反证法证明勾股定理初步 知乎




File 直角三角形與畢氏定理 Jpg Wikimedia Commons



直角三角形高度毕达哥拉斯定理 直角三角形png图片素材免费下载 图片编号 Png素材网




3种方法来求直角三角形斜边的长度



Search Q E7 Ad E8 85 B0 E4 B8 E8 92 E5 Tbm Isch




直角三角形斜边中线定理的证明 红橙教育网



直角三角形边长 图片欣赏中心 急不急图文 Jpjww Com
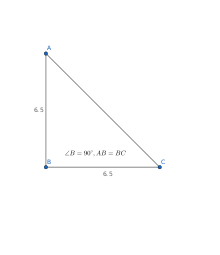



三角形 维基百科 自由的百科全书
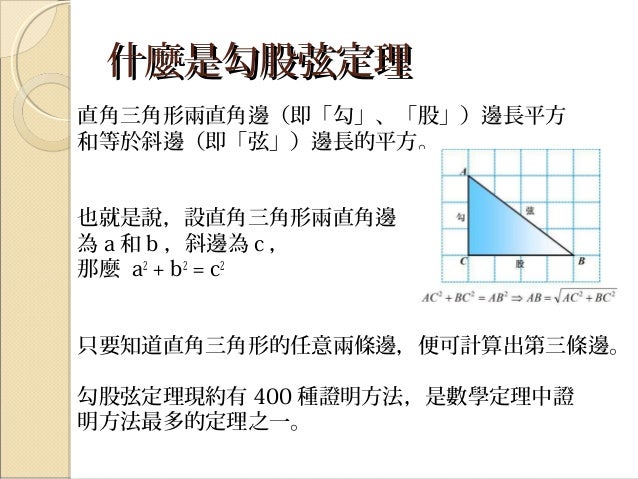



畢氏定理




直角三角形斜邊中線定理 直角三角形斜邊中線定理是數學中關於直角三角形的一 百科知識中文網



斜边怎么算三角形的斜边怎么算 朵拉利品网
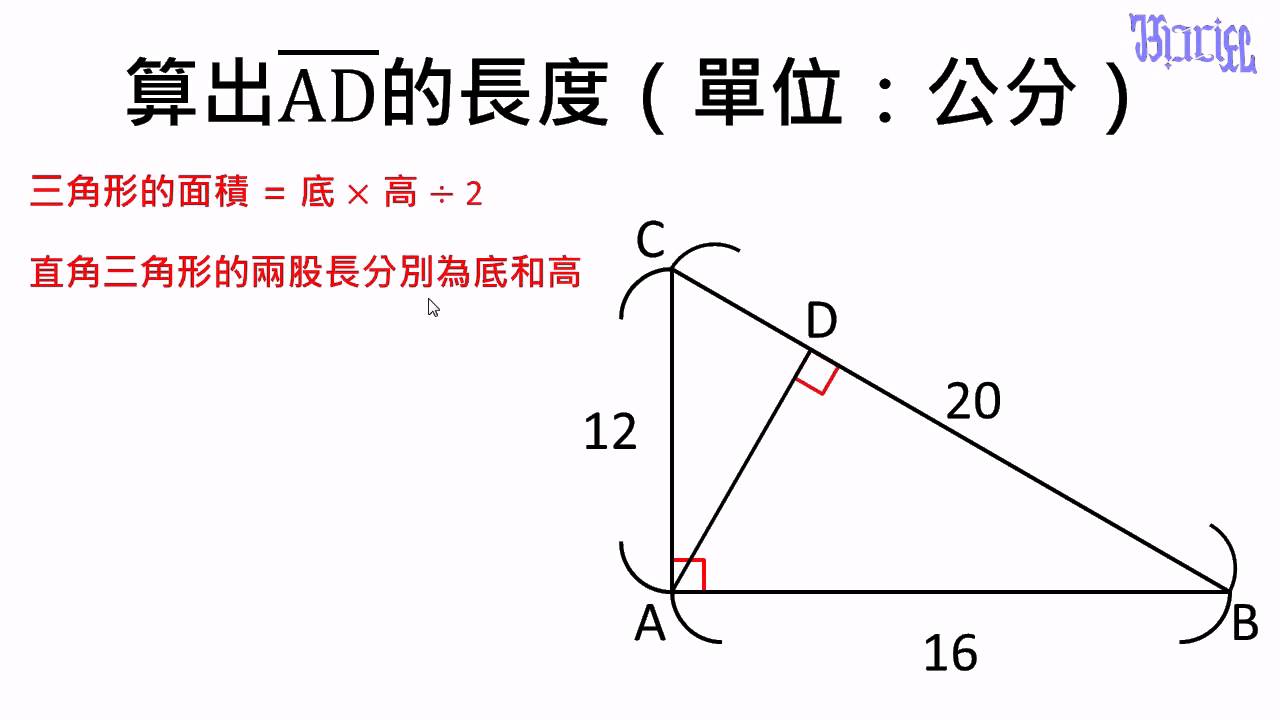



三角形 22 直角三角形面積的進階計算題 Youtube




圖解數學 一張圖說明白 直角三角形與勾股定理 每日頭條



直角三角形全等判定定理 宏观视界



天天快报



勾股定理的计算方法 推荐



用勾股定理证明锐角三角形




如何使用勾股定理 12 步骤




直角三角形斜边中线定理 搜狗百科




怎么求直角三角形斜边的长度 生活百科
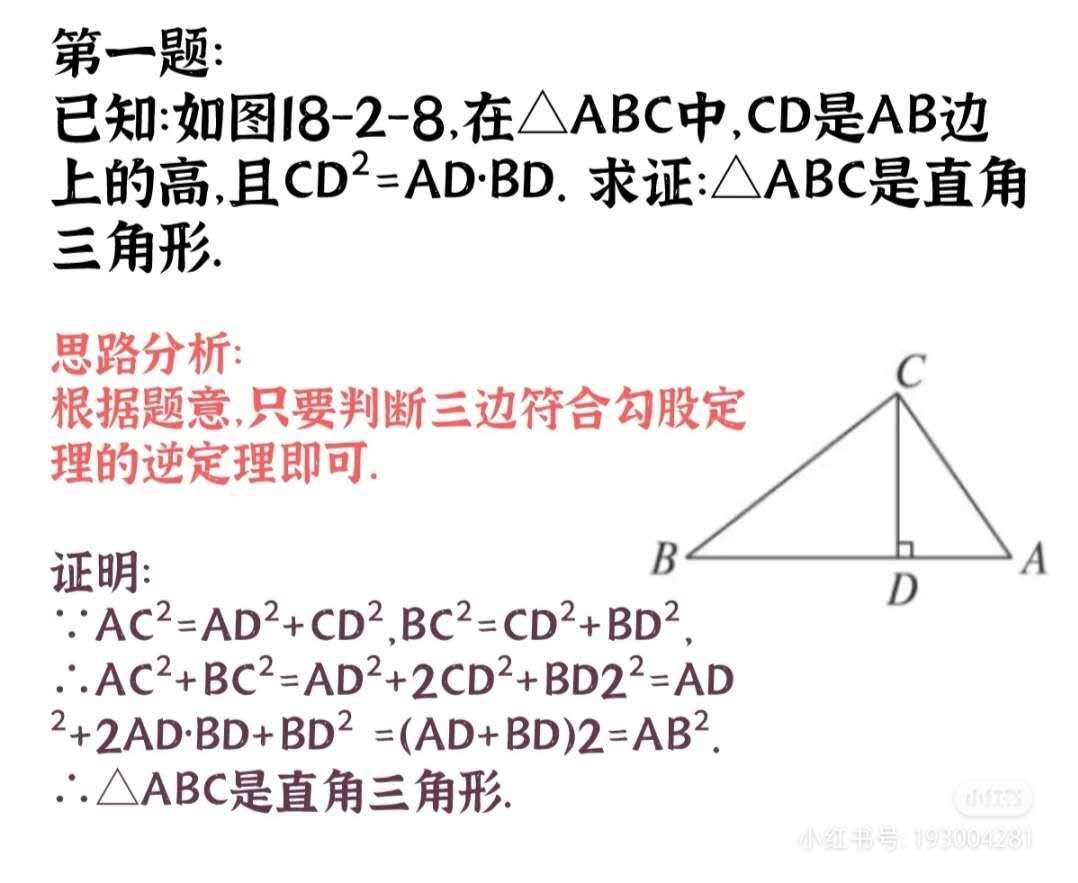



初中数学 勾股定理50道经典例题 1 知乎



吴国平 中国最早发现勾股定理 但西方为何不承认




爱因斯坦相对论证明勾股定理 人教版教材亮了 6park Com
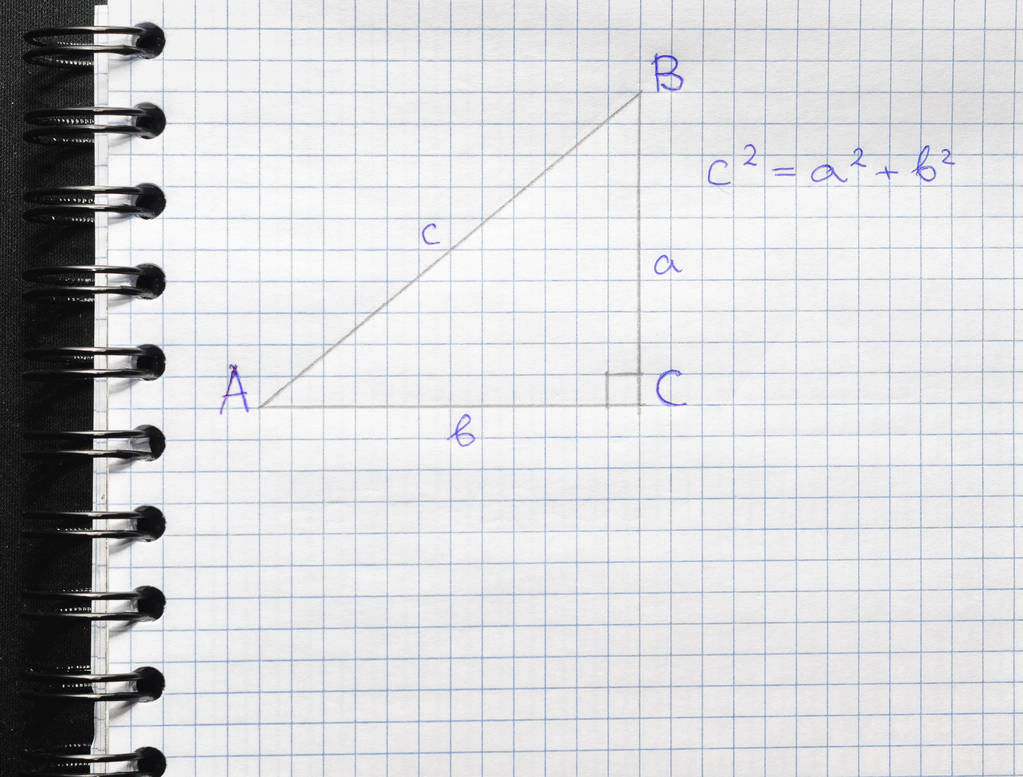



已知直角三角形三边长



1




用四个全等的直角三角形 通过拼图的方法验证勾股定理有几种方法 雨露学习互助



哪些定理或性质与三角形的中点有关 会有哪些常见经典考试题型 初中数学 学习资料大全 免费学习资源下载



家合教育 中考数学知识点 直角三角形及勾股定理 考查



勾股定理怎么算 科普 常识知识




Ppt 第二节直角三角形 一 Powerpoint Presentation Free Download Id



悟空问答 关于勾股定理 有哪些有趣的题目 7个回答



1 3 直角三角形全等的判定 Page19 湘教版八年级数学下册电子课本 教材 教科书 好多电子课本网



求直角三角形斜边长直角三角形求斜边长计算公式 朵拉利品网




直角三角形 维基百科 自由的百科全书



直角三角形面积怎么算性质是什么 初三网



直角三角形勾股定理公式 直角三角形勾股定理公式表 三角形勾股定理公式 智流金融网



在30度 45度的直角三角形中 它们勾股定理的三边长的比值分别是什么 作业 慧海网



八年级下勾股定理 判定直角三角形的方法专题 初中数学 学习资料大全 免费学习资源下载




直角三角形斜边高公式 直角三角形斜边长怎么算 三人行教育网 Www 3rxing Org




常見的直角三角形之三邊長比 畢氏數 勾股數 Live 多媒體數學觀念典online



0 件のコメント:
コメントを投稿